My Projects

FastVPINNs
Fast and efficient hp-Variational Physics-Informed Neural Networks for solving PDEs
We propose a novel tensor based method to compute variational loss, which leads to 100x speedup in training time when compared to the existing implementations.
Read More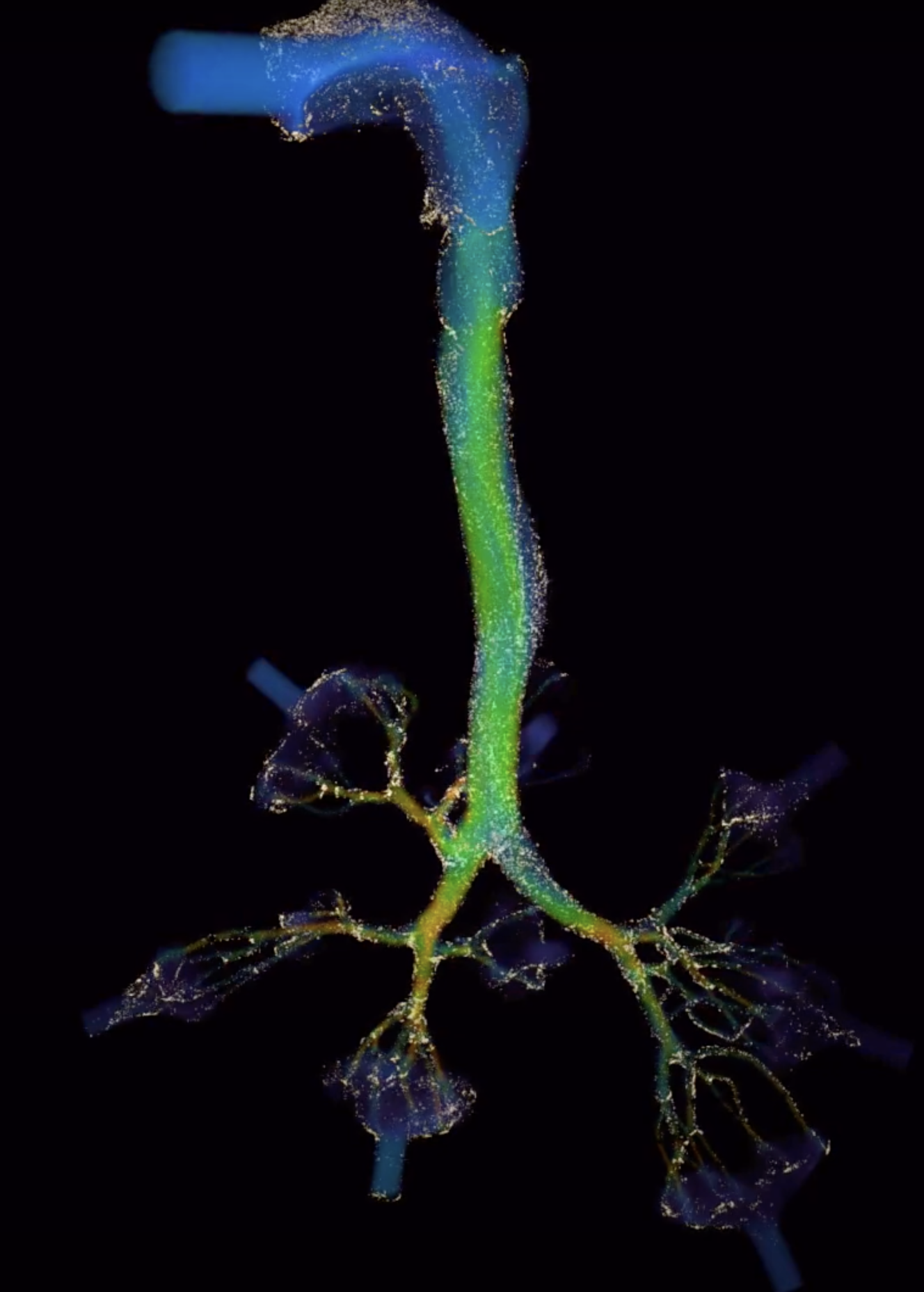
GPU-Accelerated particle tracking
FEM based Lagrangian particle tracking in Human air pathways
We have implemented a GPU accelerated FEM solver for Lagrangian particle tracking in human air pathways. The framework is implemented in CUDA using the FEM library ParMooN. We achieved a speed up of 80x when compared to the sequential implementation.
Read More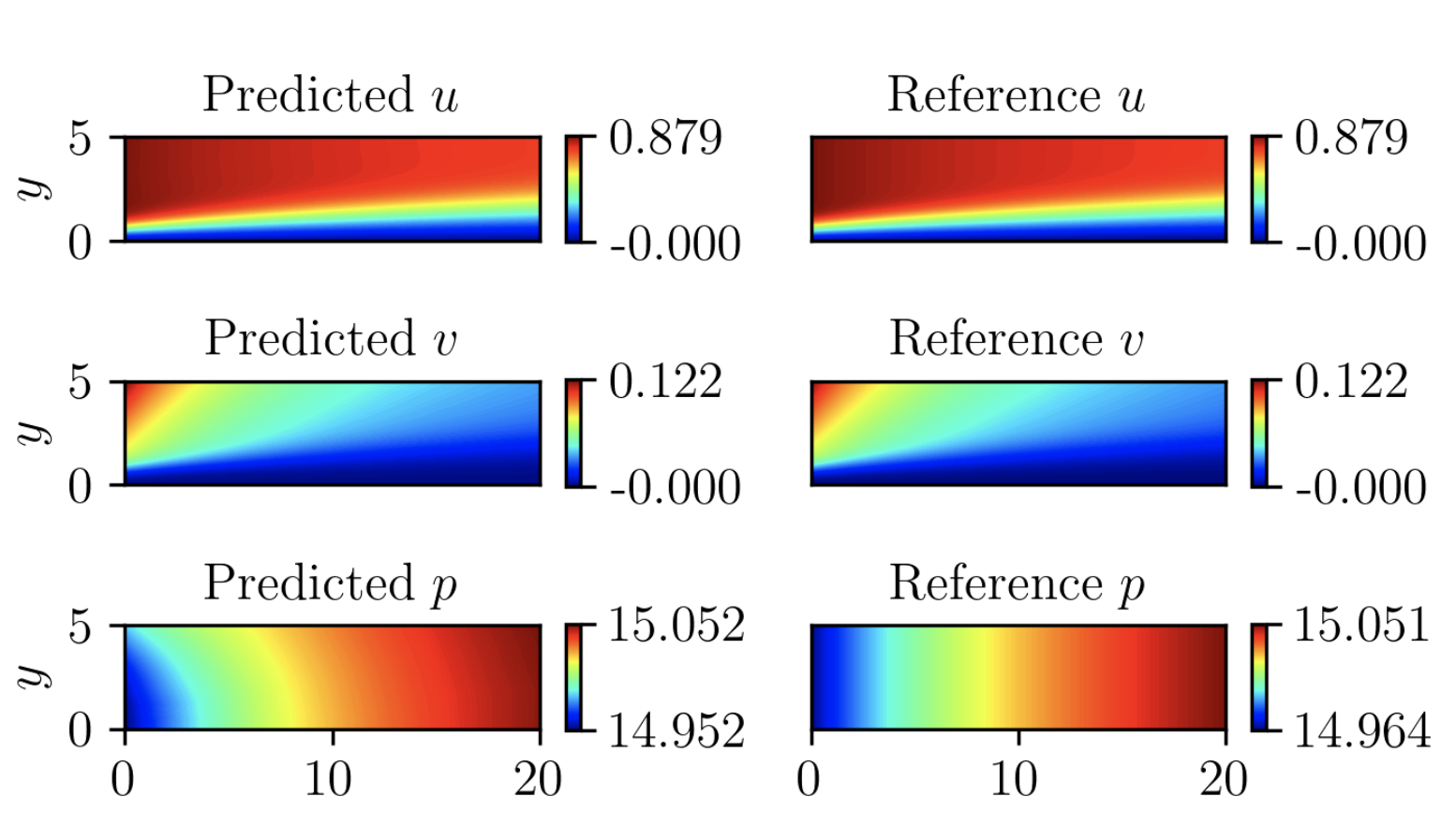
hp-VPINNs for Incompressible Navier-Stokes Equations
FastVPINNs implementation for vector valued problems
We extend the implemetation of hp-VPINNs for vector valued problems, such as Burgers equation and the incompressible Navier-Stokes equations. We have solved Lid-Driven Cavity, flow past a cylinder, Falkner-Skan boundary layer flow problems etc. We have achieved a 2.4x speedup in training time when compared to the existing PINNsimplementations.
Read More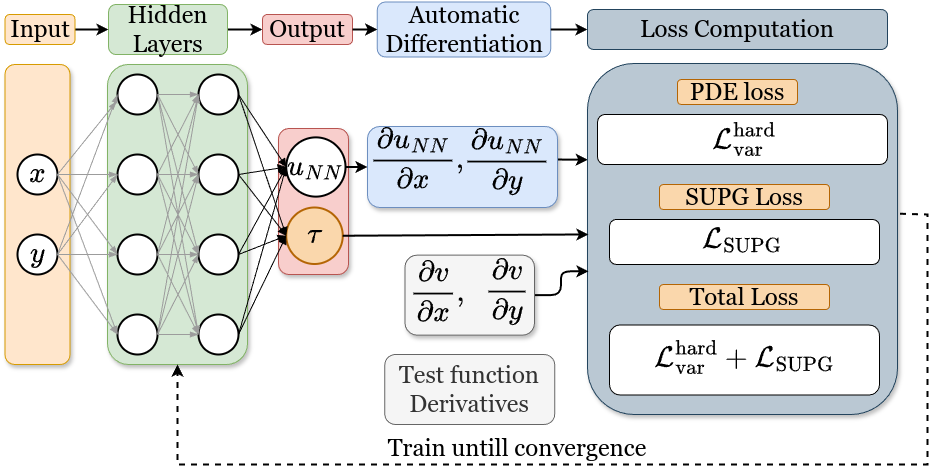
Improving hp-Variational Physics-Informed Neural Networks for Steady-State Convection-Dominated Problems
New Methods to improve accuracy of variational PINNs in solving Singularly Perturbed Problems.
We present an ensemble forecast for Wave-3 of COVID-19 in the state of Karnataka, India, using the IISc Population Balance Model for infectious disease spread. The reported data of confirmed, recovered, and deceased cases in Karnataka from 1 July 2020 to 4 July 2021 is utilized to tune the model’s parameters, and an ensemble forecast is done from 5 July 2021 to 30 June 2022. The ensemble is built with 972 members by varying seven critical parameters that quantify the uncertainty in the spread dynamics (antibody waning, viral mutation) and interventions (pharmaceutical, non-pharmaceutical). The probability of Wave-3, the peak date distribution, and the peak caseload distribution are estimated from the ensemble forecast.
Read More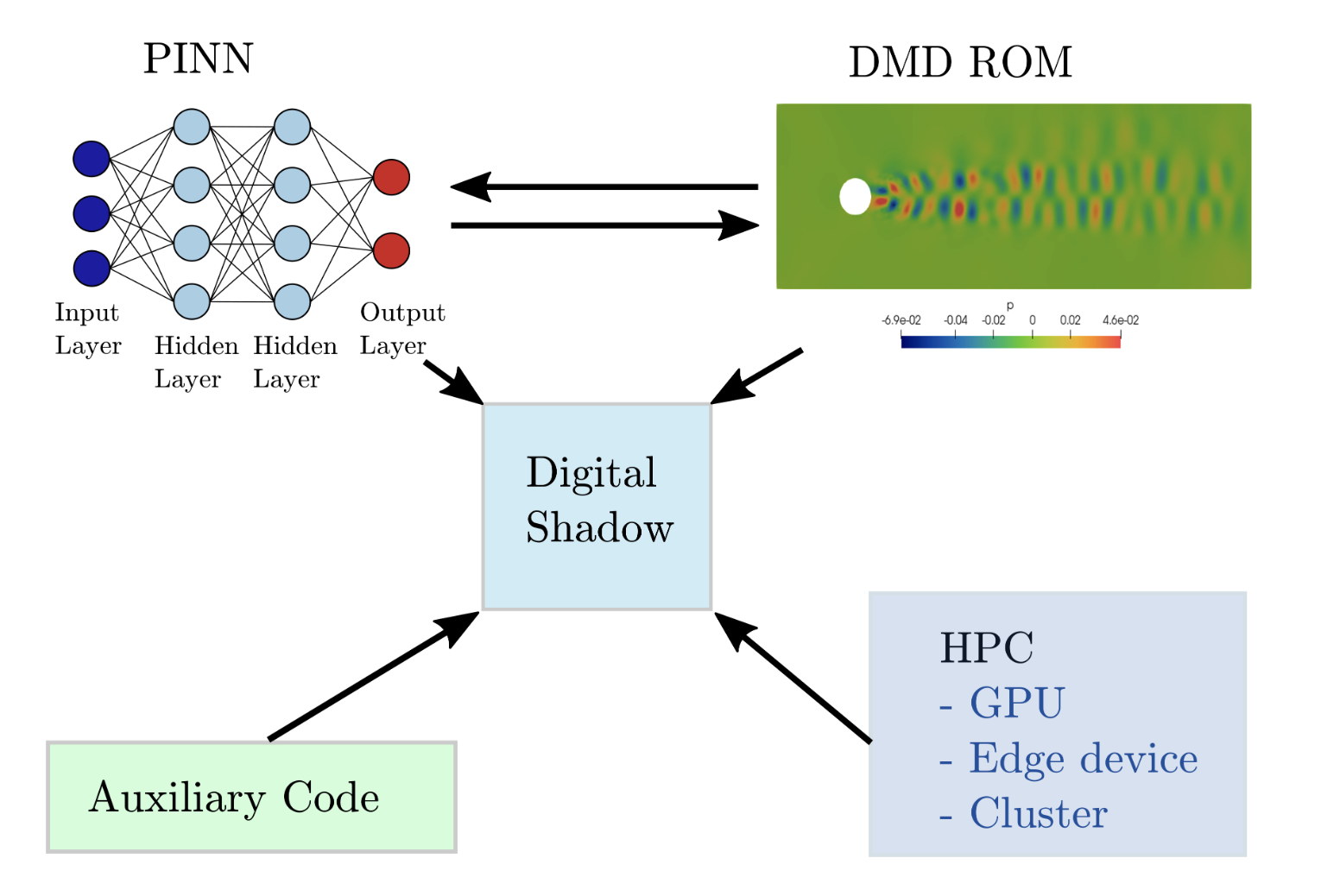
Digital Shadowing
PINNs + DMD based framework for realtime moitoring of wind farms
We present a novel simulation framework that combines Physics Informed Neural Networks (PINNs) with Dynamic Mode Decomposition (DMD) for rapid fluid flow simulations in complex domains. This lightweight, flexible framework is designed to create simulation-based Digital Twins, primarily targeting wind farm aerodynamics but adaptable to other continuous physics systems. By incorporating a reduced order model, the framework aims to enable trained models to run efficiently on compact edge devices, as demonstrated through a transient heat transfer example.
Read More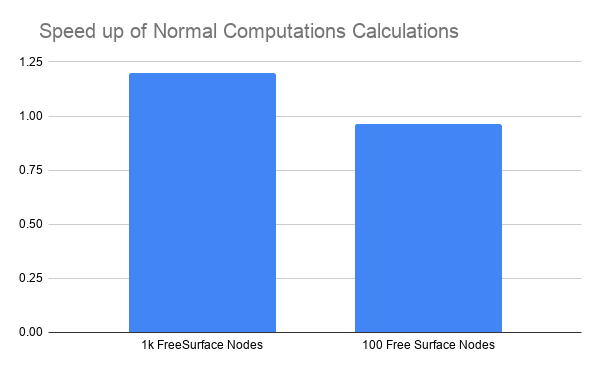
Asynchronous Mesh Movement - GPU
Parallel Asynchronous Mesh Movement Computations for ALE-FEM in GPU
This project optimizes mesh movement computations for Navier-Stokes solvers by leveraging GPU parallelism. We addressed two key challenges: restructuring module dependencies to enable asynchronous GPU computation, and efficiently transferring complex finite element data structures between CPU and GPU using mapped arrays. These innovations allow for seamless GPU computations without host intervention, significantly enhancing overall solver performance.
Read More
ALE-FEM for Free Surface Flows
Arbitrary Lagrangian Eulerian based FEM for Free Surface Flows in 3D
Simulations of free surface flow of an incompressible fluid using ALE-FEM. The implementation is done in our in-house FEM library ParMooN.
Read More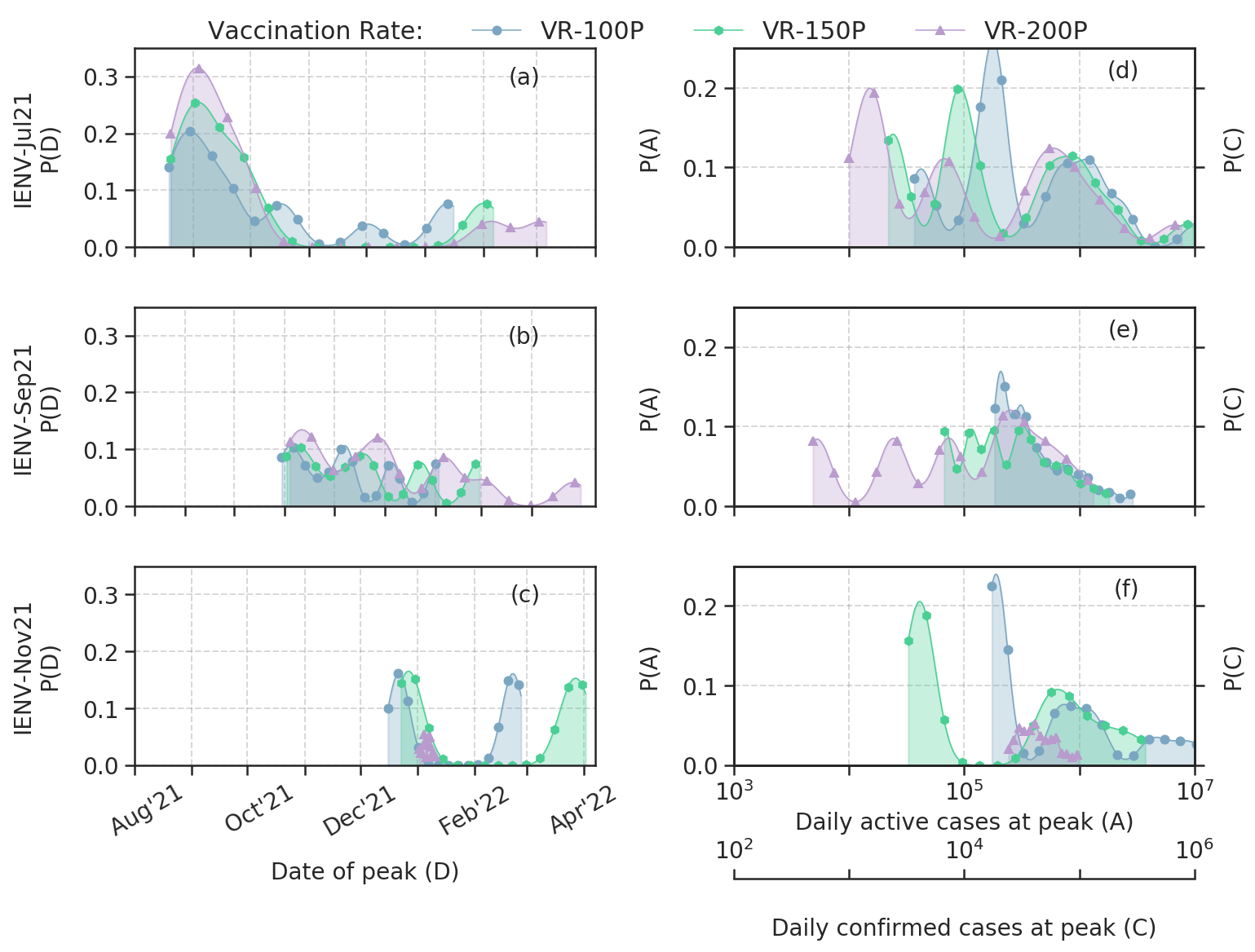
Ensemble forecast of COVID-19 in Karnataka for vulnerability assessment and policy interventions
Population balance model to predict the severity of Covid second wave 3
We present an ensemble forecast for Wave-3 of COVID-19 in the state of Karnataka, India, using the IISc Population Balance Model for infectious disease spread. The reported data of confirmed, recovered, and deceased cases in Karnataka from 1 July 2020 to 4 July 2021 is utilized to tune the model’s parameters, and an ensemble forecast is done from 5 July 2021 to 30 June 2022. The ensemble is built with 972 members by varying seven critical parameters that quantify the uncertainty in the spread dynamics (antibody waning, viral mutation) and interventions (pharmaceutical, non-pharmaceutical). The probability of Wave-3, the peak date distribution, and the peak caseload distribution are estimated from the ensemble forecast.
Read More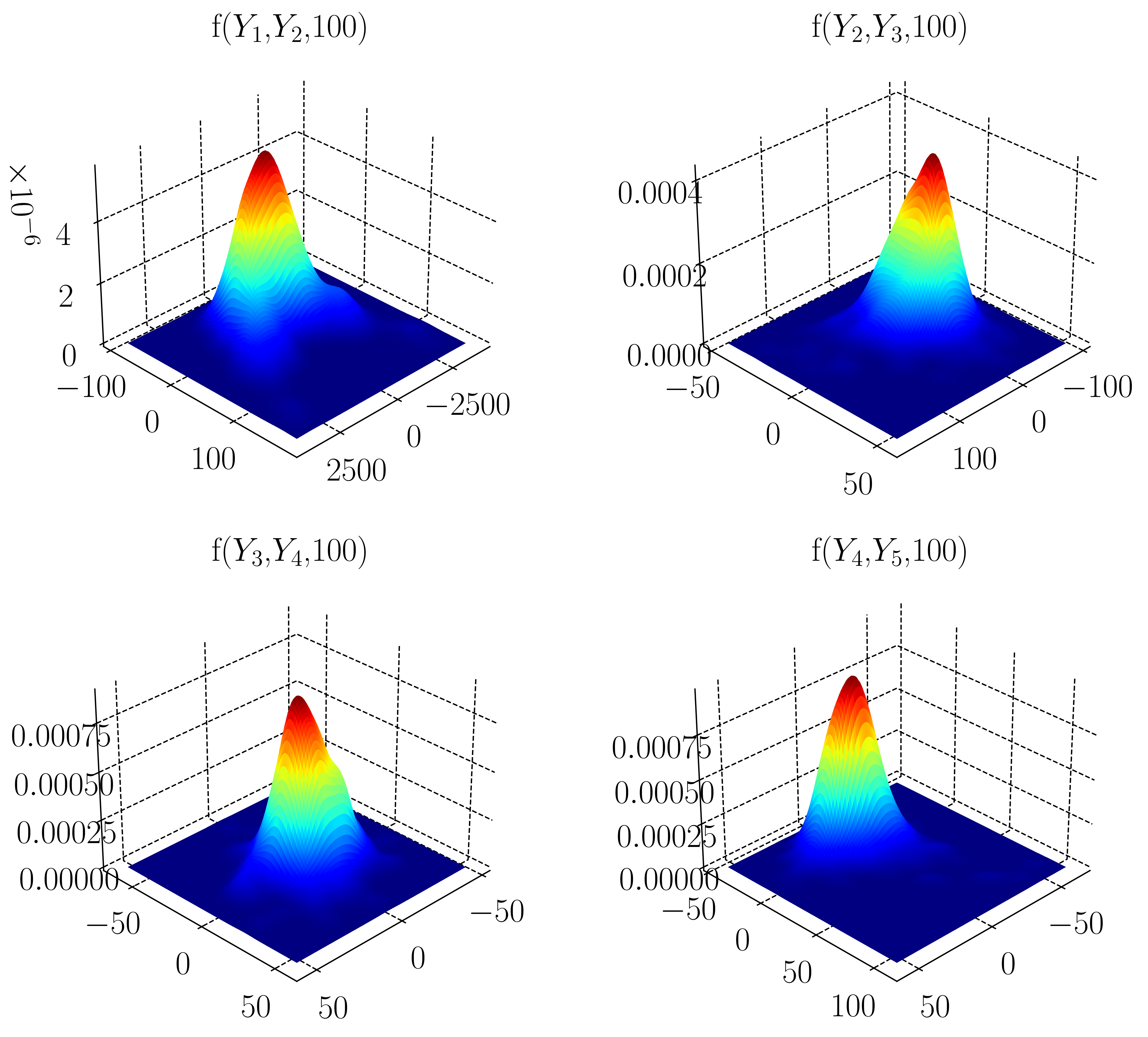
A finite element implementation of the dynamically orthogonal field equations scheme for uncertainty quantification
Dynamic Orthogonal formulation for Uncertanity Quantification using FEM
In this work, we employ an efficient and provably accurate Dynamically Orthogonal (DO) field equation method for reducing the stochastic order by ensuring that the mean squared error of the variance of the stochastic field is minimised. By hypothesizing a decomposition of the solution field into a mean and stochastic dynamical component, we derive a system of field equations consisting of a Partial Differential Equation (PDE) for the mean field, a family of PDEs for the orthonormal basis that describe the stochastic subspace where the stochasticity ‘lives’ as well as a system of Stochastic Differential Equations that defines how the stochasticity evolves in the time varying stochastic subspace. These new evolution equations are derived directly from the original SPDE, using nothing more than a dynamically orthogonal condition on the representation of the solution. We apply this method to both linear and non-linear dynamical systems and compare our results with Monte Carlo simulations.